Skip to main content

Geographic and Projected Coordinate Systems

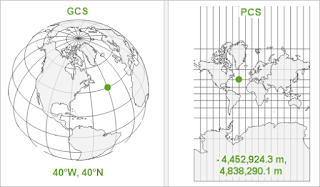
Geographic Coordinate System (GCS)

A Geographic Coordinate System (GCS) uses a three-dimensional spherical surface to define locations on Earth. It is based on a datum, an ellipsoid, and angular units (latitude and longitude).

Key Components of GCS:

  • Latitude (ϕ): Measures the north-south position relative to the Equator (0°). It ranges from 90°N to 90°S.
  • Longitude (λ): Measures the east-west position relative to the Prime Meridian (0°). It ranges from 180°E to 180°W.
  • Datum: Defines the reference ellipsoid and origin point.
  • Ellipsoid: An approximation of the Earth's shape.
  • Geoid: A model of Earth's gravitational surface.

Example of a Geographic Coordinate System:

  • WGS 84 (World Geodetic System 1984) – Used in GPS and global mapping applications.

Advantages of GCS:

  • Accurately represents global locations.
  • Commonly used for spatial data storage and sharing.

Disadvantages of GCS:

  • Distances and areas are distorted because the Earth is not a perfect sphere.
  • Not ideal for detailed, local mapping due to distortions in scale.

Projected Coordinate System (PCS)

A Projected Coordinate System (PCS) is a two-dimensional representation of Earth's surface created by mathematically transforming the curved surface of the Earth onto a flat plane.

Key Components of PCS:

  • Projection Type: Defines how the Earth's surface is transformed.
  • X, Y Coordinates: Express positions in meters or feet instead of latitude and longitude.
  • Origin and Datum: Ensures projection accuracy.

Types of Projections in PCS:

  1. Conformal Projection: Preserves shape but distorts area (e.g., Mercator projection).
  2. Equal-Area Projection: Maintains area but distorts shape (e.g., Albers Equal-Area).
  3. Equidistant Projection: Preserves distances along specific lines (e.g., Plate Carrée).
  4. Azimuthal Projection: Maintains direction but distorts distance (e.g., Lambert Azimuthal Equal Area).

Example of a Projected Coordinate System:

  • UTM (Universal Transverse Mercator): Divides the world into 60 zones, each 6° wide.
  • State Plane Coordinate System (SPCS): Used for high-accuracy local mapping in the U.S.

Advantages of PCS:

  • Preserves distances and areas, making it ideal for local and regional mapping.
  • Allows for easier measurements and calculations in GIS.

Disadvantages of PCS:

  • Distortion increases when used for large-scale or global mapping.
  • Different projections may be required for different regions.

Datums in GIS

A datum is a mathematical model that defines the size, shape, and orientation of the Earth for mapping and surveying purposes.

Types of Datums:

A. Geodetic Datums (Horizontal Datums)

Used for positioning locations on the Earth's surface.

  • Global Datums:

    • WGS 84: Used in GPS and most global applications.
    • ITRF (International Terrestrial Reference Frame): Used for scientific measurements.

  • Local Datums:

    • NAD 27 (North American Datum 1927): Based on Clarke 1866 Ellipsoid, used in North America.
    • NAD 83 (North American Datum 1983): Updated to align with modern satellite data.

B. Vertical Datums

Used for measuring elevations and depths.

  • Geoid-Based:

    • EGM96 (Earth Gravitational Model 1996): Used for global height measurements.
    • NAVD88 (North American Vertical Datum 1988): Used in North America.

  • Ellipsoid-Based:

    • WGS 84 Ellipsoid Height: Used in GPS applications.

Example:

  • A point in New York City might have different coordinates in WGS 84 versus NAD 83 due to differences in datum definitions.

Ellipsoid and Geoid in GIS

These are models of Earth's shape used in geodesy and GIS.

Ellipsoid

  • A mathematically defined smooth surface that approximates the shape of the Earth.
  • Used in map projections and coordinate systems.
  • Example: GRS 80 (Geodetic Reference System 1980), WGS 84.

Geoid

  • Represents the actual shape of the Earth based on gravity measurements.
  • More accurate for elevation measurements than ellipsoids.
  • Example: EGM2008 (Earth Gravitational Model 2008).

Key Differences:

FeatureEllipsoidGeoid
DefinitionSmooth mathematical model of EarthRealistic Earth shape based on gravity
PurposeUsed for mapping and coordinate systemsUsed for measuring precise elevations
ExampleWGS 84, GRS 80EGM96, NAVD88

Example in GIS:

  • GPS uses an ellipsoid model (WGS 84) for positioning.
  • Elevation data often references the geoid (EGM96) for height measurements.


  • GCS (Latitude-Longitude) is best for global positioning but introduces distortions.
  • PCS (Projected X-Y coordinates) is ideal for precise local measurements.
  • Datums define how coordinates align with Earth's shape.
  • Ellipsoids approximate Earth's smooth shape, while geoids account for gravitational variations.

Practical Applications in GIS:

  • GPS Navigation: Uses WGS 84 for positioning.
  • Land Surveys: Use local datums like NAD 83 for high-accuracy mapping.
  • Elevation Mapping: Uses geoid-based vertical datums for terrain analysis.
  • Urban Planning: Uses UTM projections for detailed city mapping.

Comments

Post a Comment

Popular posts from this blog

Photogrammetry – Types of Photographs

In photogrammetry, aerial photographs are categorized based on camera orientation , coverage , and spectral sensitivity . Below is a breakdown of the major types: 1️⃣ Based on Camera Axis Orientation Type Description Key Feature Vertical Photo Taken with the camera axis pointing directly downward (within 3° of vertical). Used for maps and measurements Oblique Photo Taken with the camera axis tilted away from vertical. Covers more area but with distortions Low Oblique: Horizon not visible High Oblique: Horizon visible 2️⃣ Based on Number of Photos Taken Type Description Single Photo One image taken of an area Stereoscopic Pair Two overlapping photos for 3D viewing and depth analysis Strip or Mosaic Series of overlapping photos covering a long area, useful in mapping large regions 3️⃣ Based on Spectral Sensitivity Type Description Application Panchromatic Captures images in black and white General mapping Infrared (IR) Sensitive to infrared radiation Veget...
Post a Comment
Read more

Photogrammetry – Geometry of a Vertical Photograph

Photogrammetry is the science of making measurements from photographs, especially for mapping and surveying. When the camera axis is perpendicular (vertical) to the ground, the photo is called a vertical photograph , and its geometry is central to accurate mapping.  Elements of Vertical Photo Geometry In a vertical aerial photograph , the geometry is governed by the central projection principle. Here's how it works: 1. Principal Point (P) The point on the photo where the optical axis of the camera intersects the photo plane. It's the geometric center of the photo. 2. Nadir Point (N) The point on the ground directly below the camera at the time of exposure. Ideally, in a perfect vertical photo, the nadir and principal point coincide. 3. Photo Center (C) Usually coincides with the principal point in a vertical photo. 4. Ground Coordinates (X, Y, Z) Real-world (map) coordinates of objects photographed. 5. Flying Height (H) He...
Post a Comment
Read more

Raster Data Structure

Raster Data Raster data is like a digital photo made up of small squares called cells or pixels . Each cell shows something about that spot — like how high it is (elevation), how hot it is (temperature), or what kind of land it is (forest, water, etc.). Think of it like a graph paper where each box is colored to show what's there. Key Points What's in the cell? Each cell stores information — for example, "water" or "forest." Where is the cell? The cell's location comes from its place in the grid (like row 3, column 5). We don't need to store its exact coordinates. How Do We Decide a Cell's Value? Sometimes, one cell covers more than one thing (like part forest and part water). To choose one value , we can: Center Point: Use whatever feature is in the middle. Most Area: Use the feature that takes up the most space in the cell. Most Important: Use the most important feature (like a road or well), even if it...
Post a Comment
Read more

Logical Data Model in GIS

In GIS, a logical data model defines how data is structured and interrelated—independent of how it is physically stored or implemented. It serves as a blueprint for designing databases, focusing on the organization of entities, their attributes, and relationships, without tying them to a specific database technology. Key Features Abstraction : The logical model operates at an abstract level, emphasizing the conceptual structure of data rather than the technical details of storage or implementation. Entity-Attribute Relationships : It identifies key entities (objects or concepts) and their attributes (properties), as well as the logical relationships between them. Business Rules : Business logic is embedded in the model to enforce rules, constraints, and conditions that ensure data consistency and accuracy. Technology Independence : The logical model is platform-agnostic—it is not tied to any specific database system or storage format. Visual Representat...
Post a Comment
Read more

Photogrammetry

Photogrammetry is the science of taking measurements from photographs —especially to create maps, models, or 3D images of objects, land, or buildings. Imagine you take two pictures of a mountain from slightly different angles. Photogrammetry uses those photos to figure out the shape, size, and position of the mountain—just like our eyes do when we see in 3D! Concepts and Terminologies 1. Photograph A picture captured by a camera , either from the ground (terrestrial) or from above (aerial or drone). 2. Stereo Pair Two overlapping photos taken from different angles. When seen together, they help create a 3D effect —just like how two human eyes work. 3. Overlap To get a 3D model, photos must overlap each other: Forward overlap : Between two photos in a flight line (usually 60–70%) Side overlap : Between adjacent flight lines (usually 30–40%) 4. Scale The ratio of the photo size to real-world size. Example: A 1:10,000 scale photo means 1 cm on the photo...
Post a Comment
Read more